| time | topic |
|---|---|
| 3:00-3:45 | Understanding clusters in data using visualisation |
| 3:45-4:30 | Building better classification models with visual input |
Visualising High-dimensional Data with R
Dianne Cook
Monash University
Monash University
Session 2
Outline
Clustering
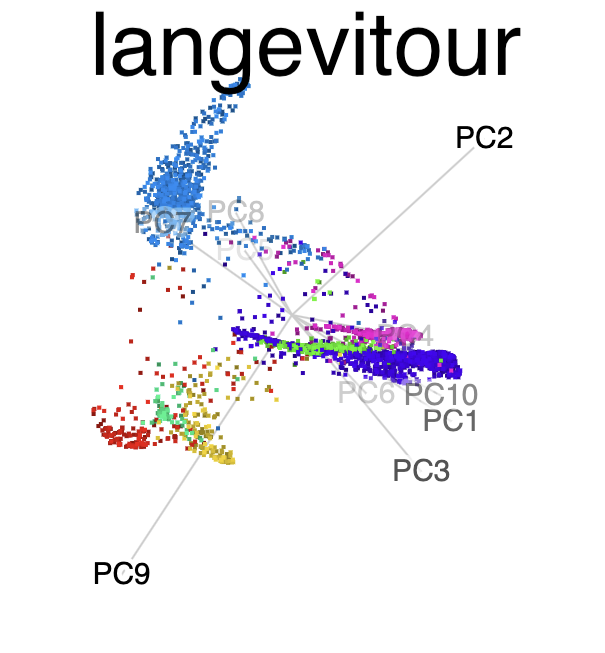
Method 1: Spin-and-brush
What are clusters?
Ideal thinking of neatly separated clusters, but it is rarely encountered in data
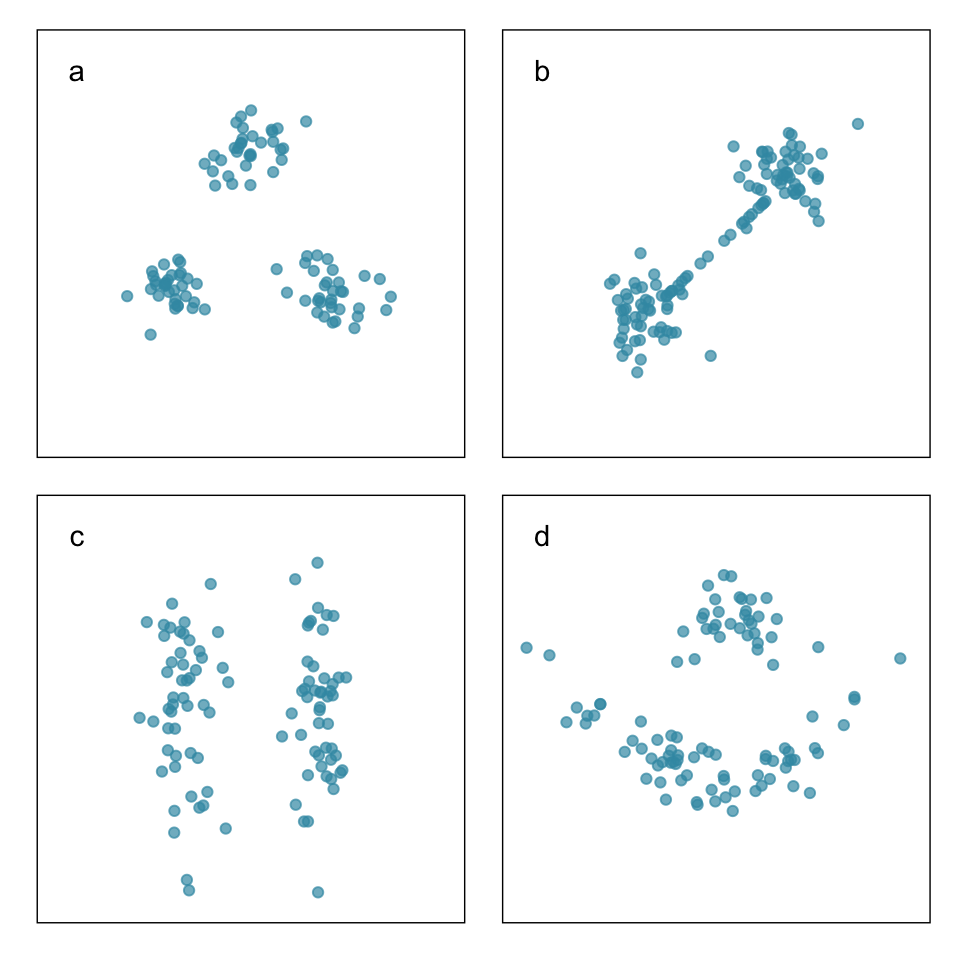
Objective is to organize the cases into groups that are similar in some way. You need a measure of similarity (or distance).
Why visualise? Which is the better?
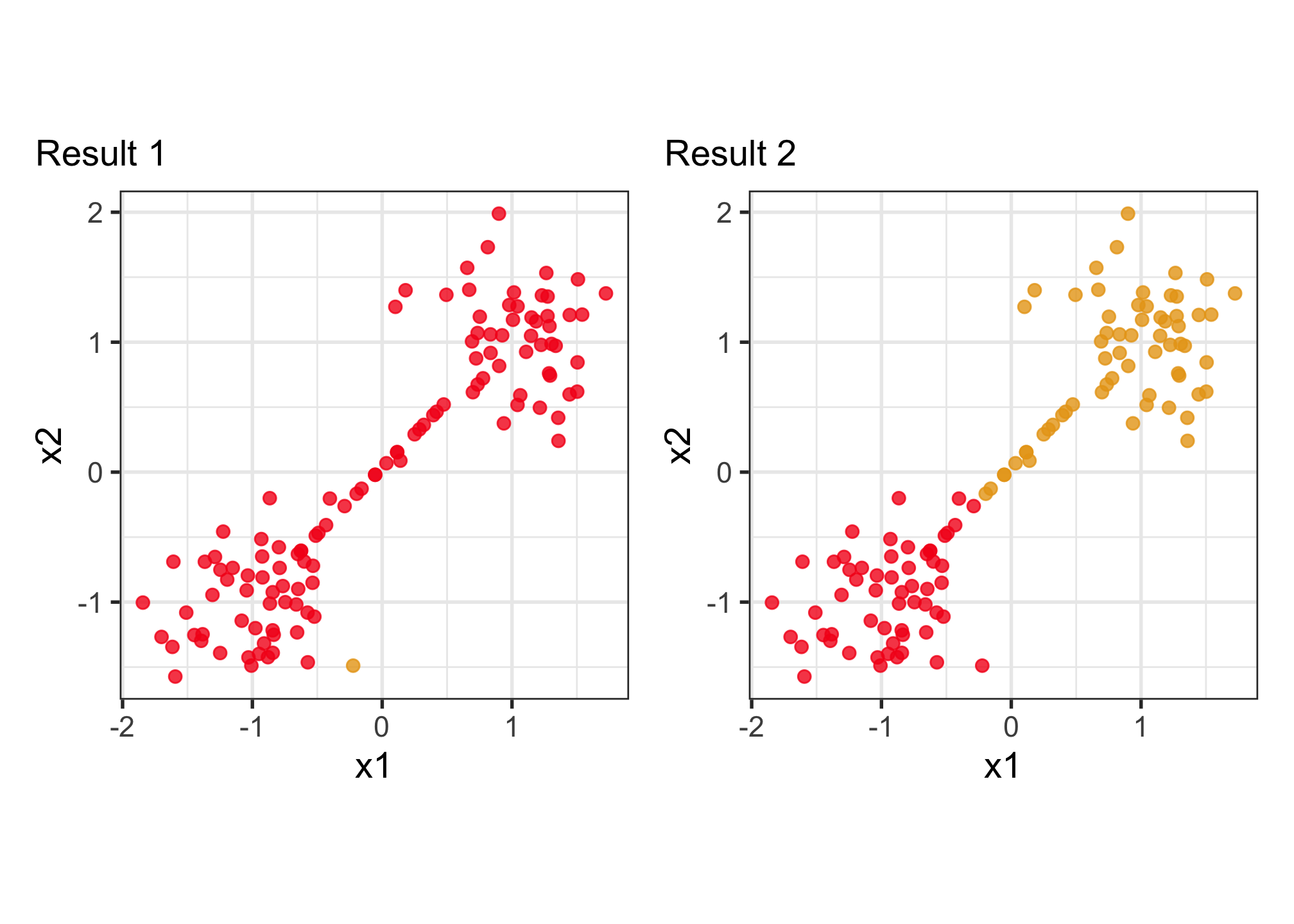
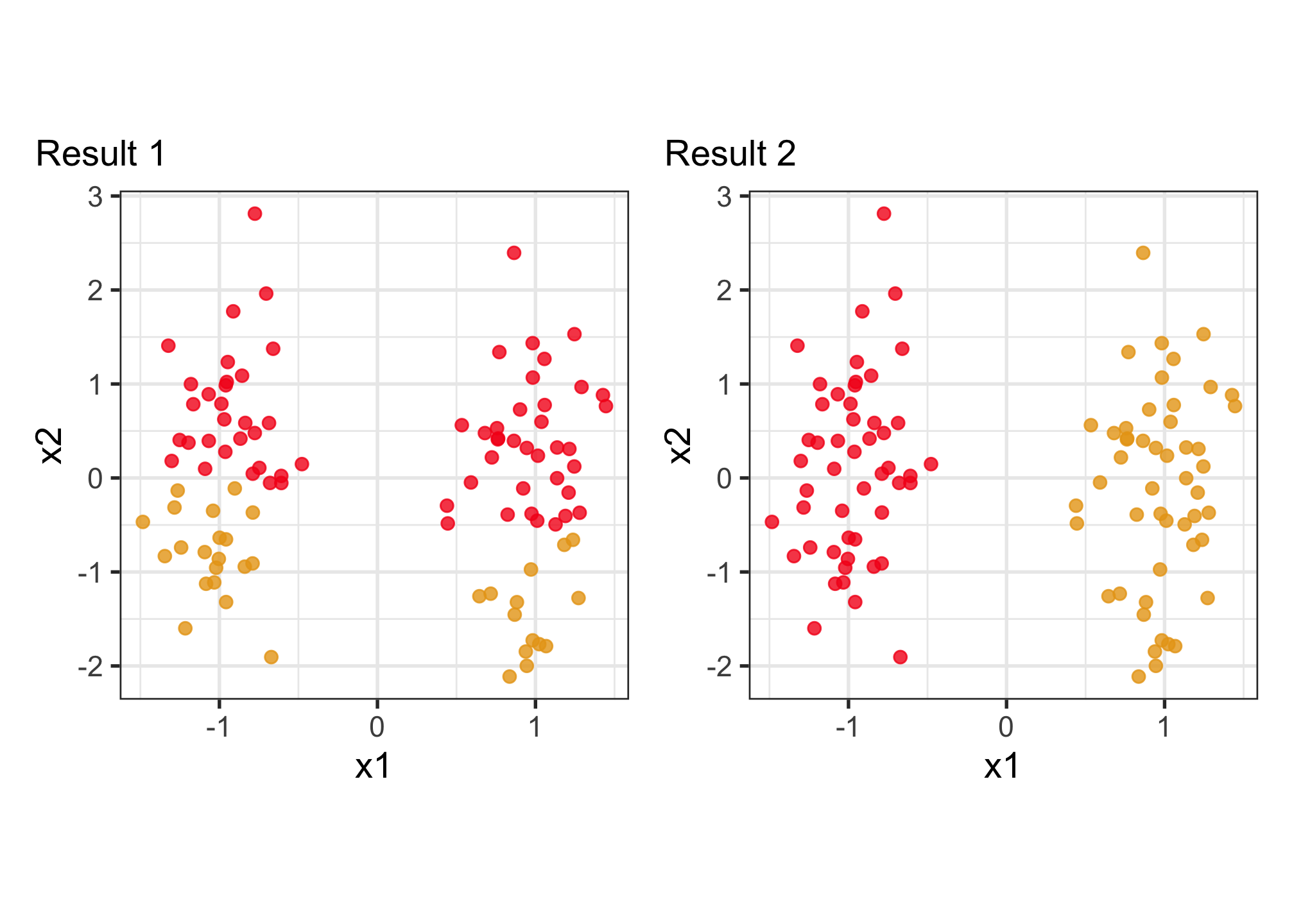
To decide on a best result, you need to see how it divides the data into clusters. The cluster statistics, like dendrogram, or cluster summaries, or gap statistics might all look good but the result is bad. You need to see the model in the data space!
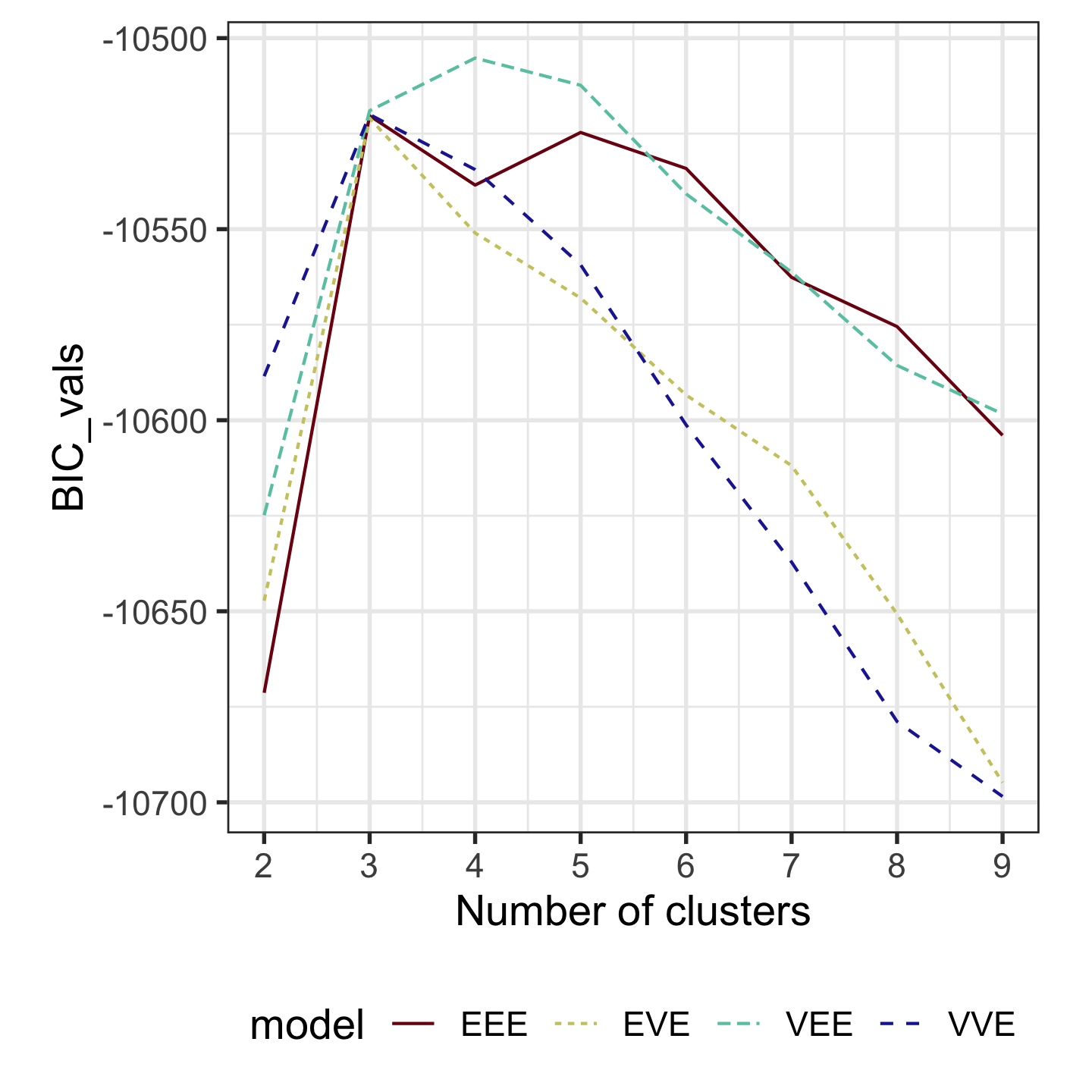
Model-based clustering (1/3)
Model-based clustering fits a multivariate normal mixture model to the data.
\[ \Sigma_k = \lambda_kD_kA_kD_k^\top, ~~~k=1, \dots, g \]
where
\(\Sigma_k\) is the variance-covariance of cluster \(k\),
\(g=\)number of clusters,
\(D_k\) describes the orientation of a cluster,
\(A_k\) describes the variance in different variables,
\(\lambda_k\) is an overall size.
Model-based clustering (2/3)
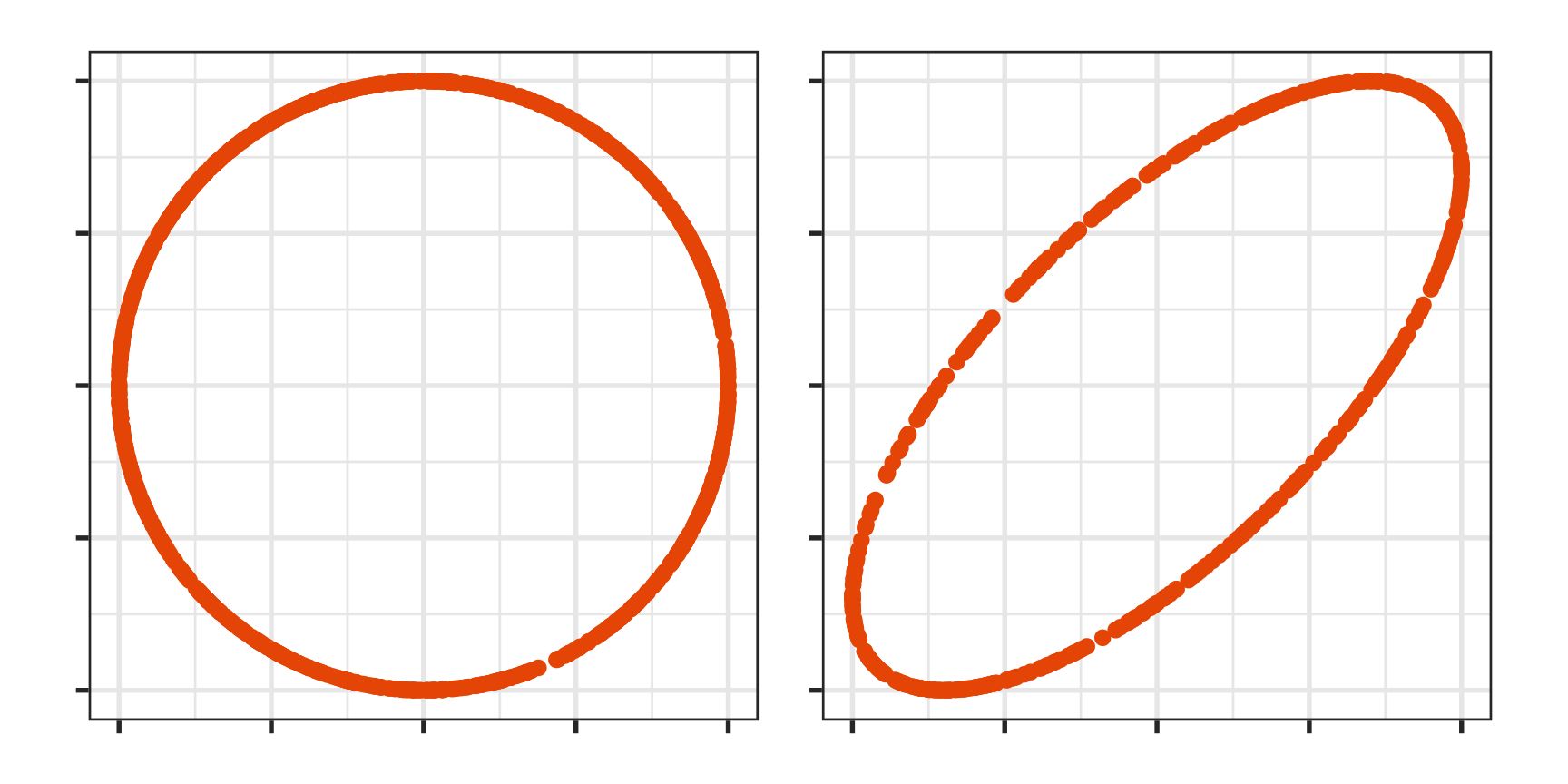
Clustering this data. What do you expect?
Can we assume the shape of the clusters is elliptical?
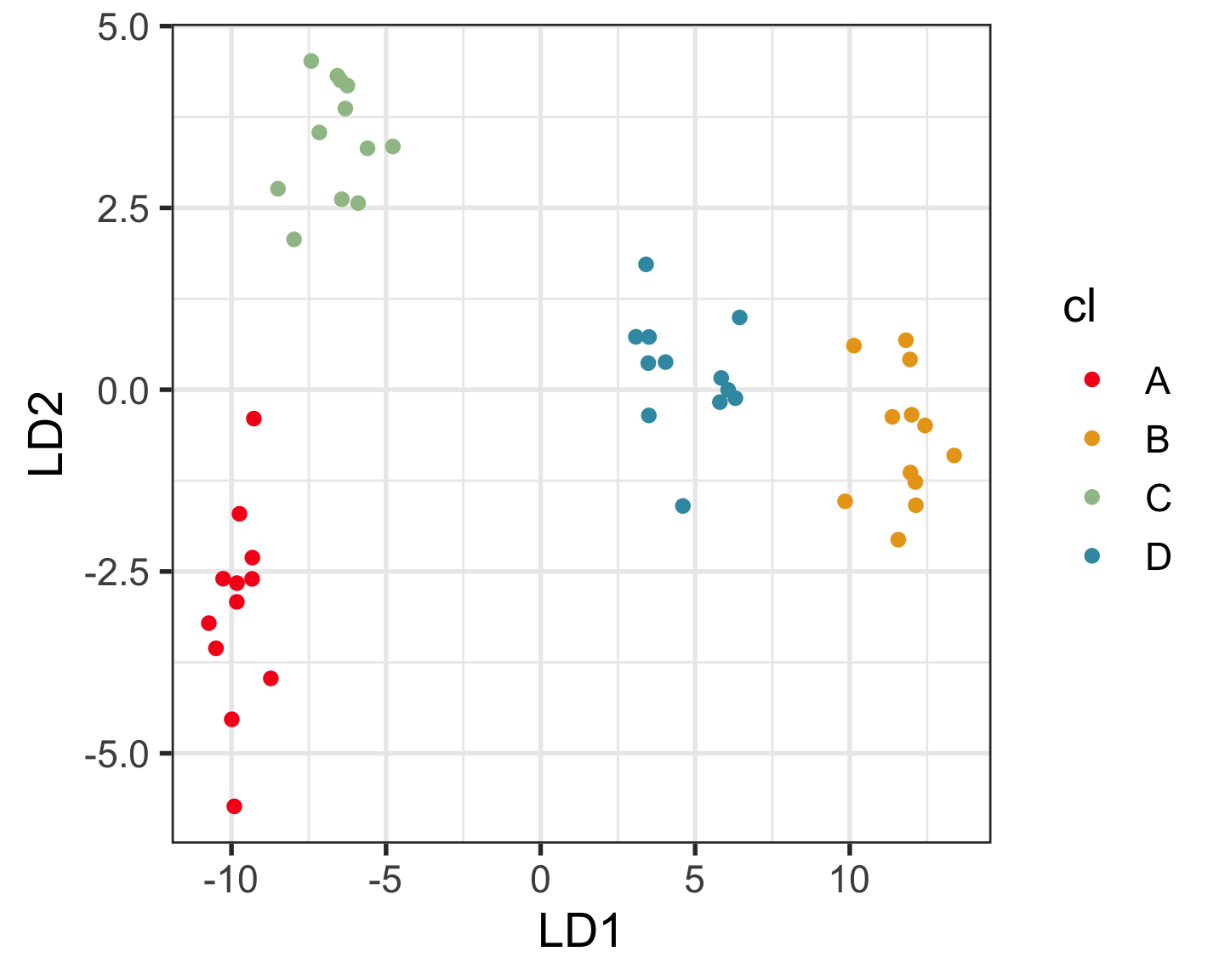
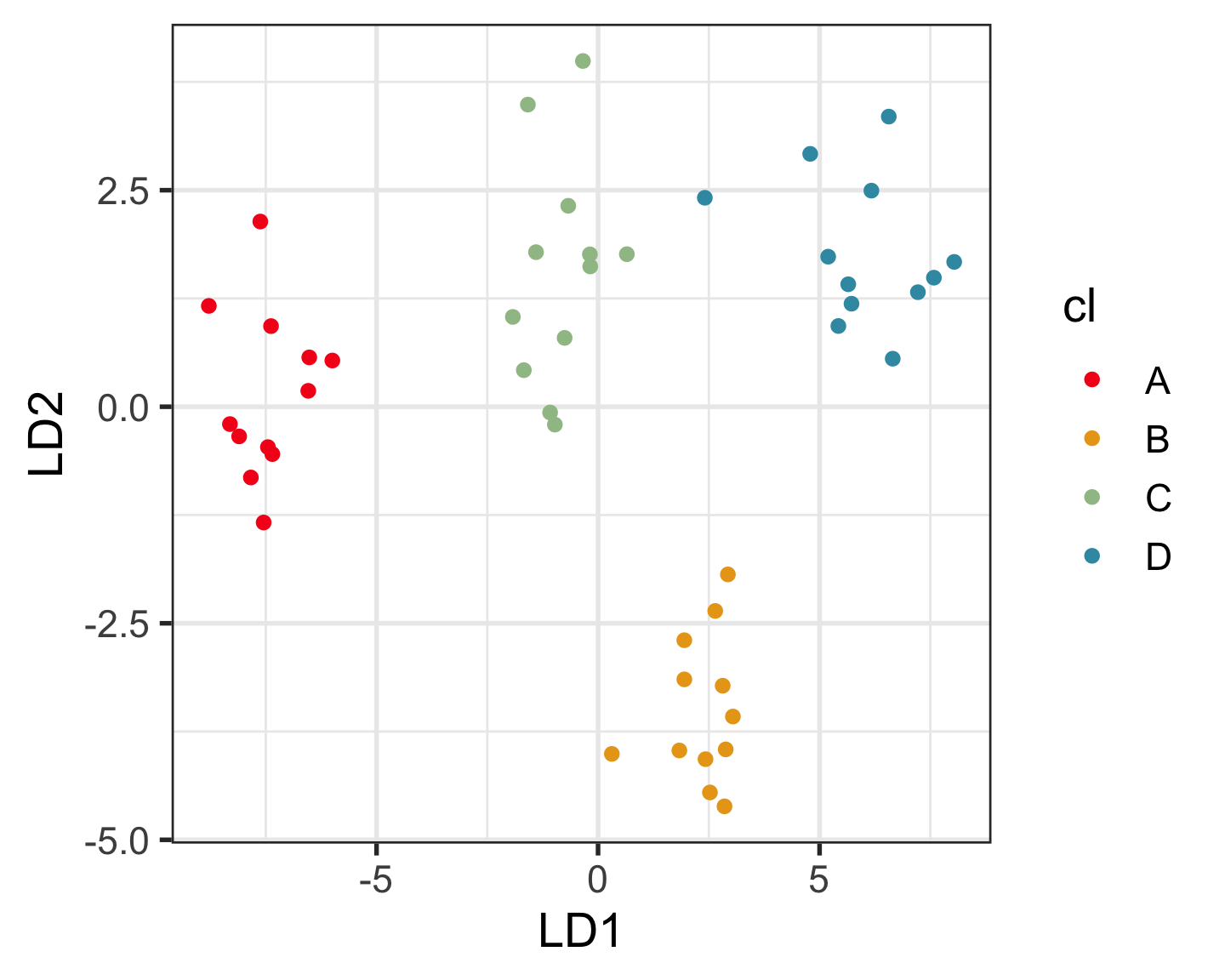
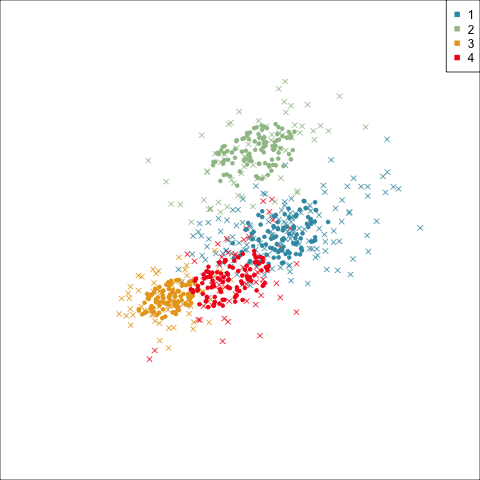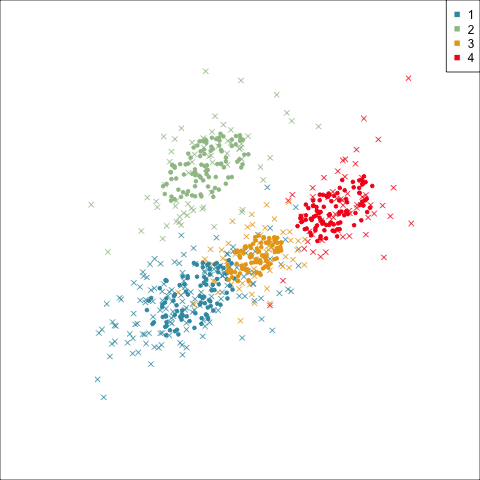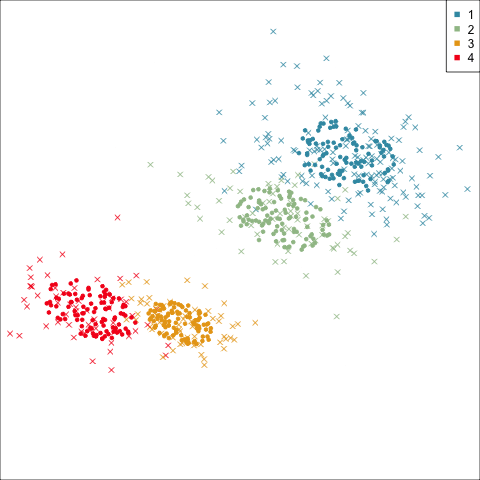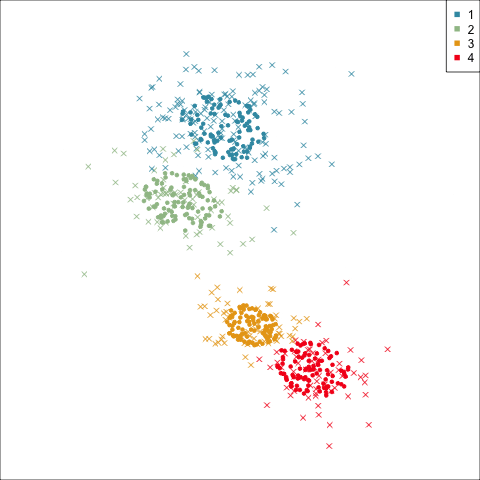
Model-based clustering (3/3)
Four-cluster VEE
Three-cluster EEE
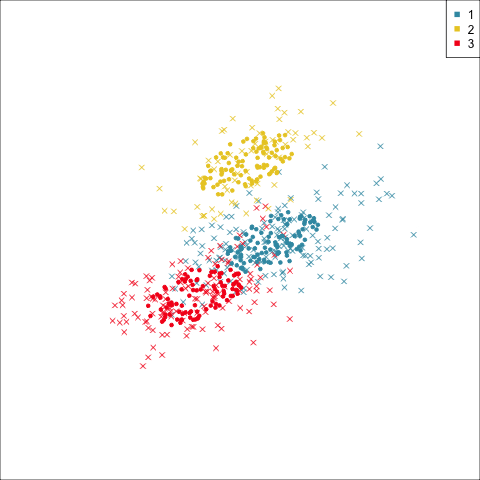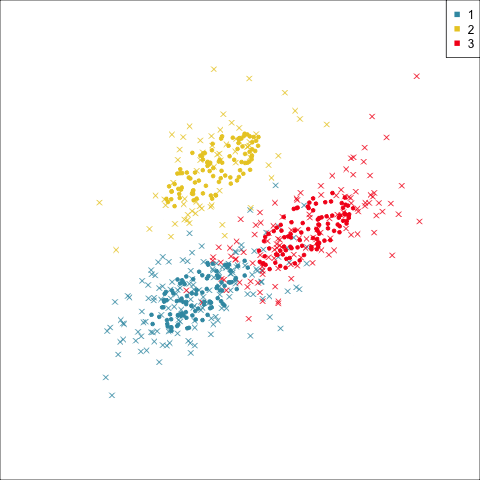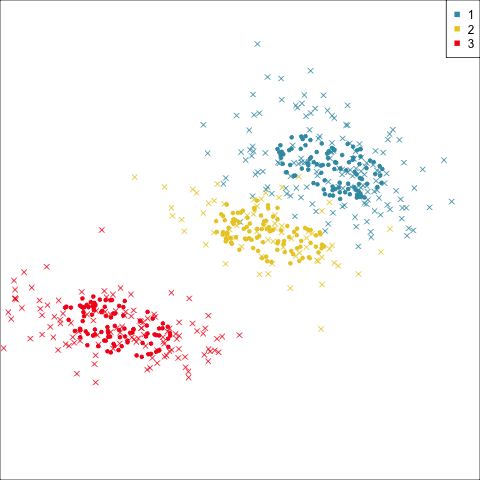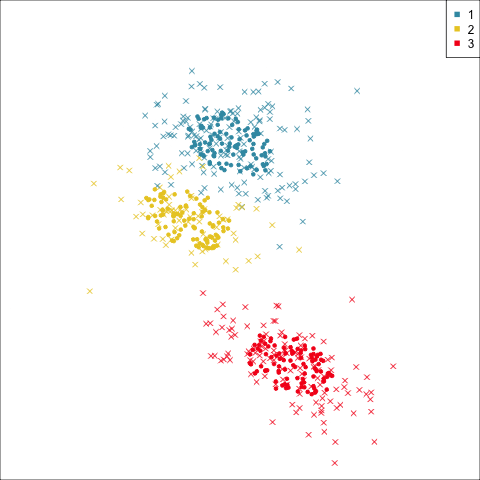
Models (ellipses) are overlaid on the data. Which is the best fit?
How do you draw ellipses in high-d?
Extract the estimated model parameters
Your turn
Use the spin-and-brush approach to extract the clusters from the c1 data.
05:00 Classification
What should you visualise?
- Understand any clustering related to the known classes.
- Obtain a sense of where boundaries might be placed.
- Examine where the fitted model fits the data well, and where poorly.
- Understand the misclassifications, whether they are reasonable given uncertainty in the data, or due to an ill-fitting or poorly specified model.
- Understand what can happen with model fitting and pattern recognition with sparse data.
Example: Linear DA
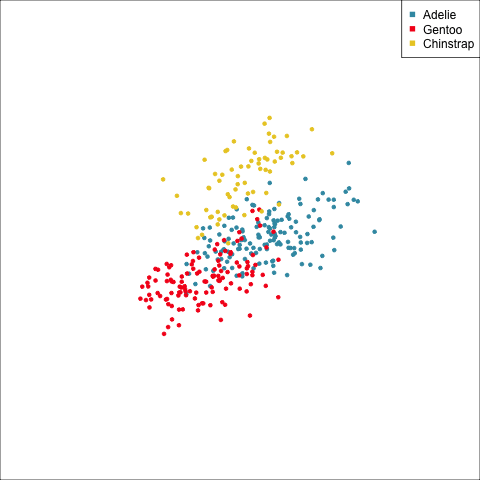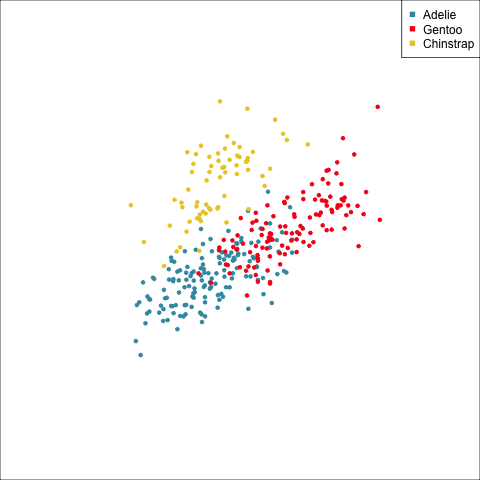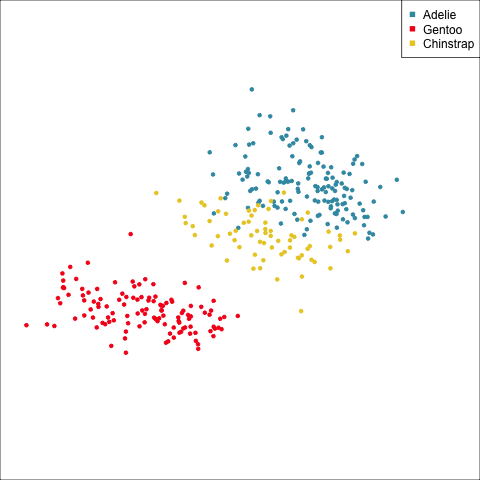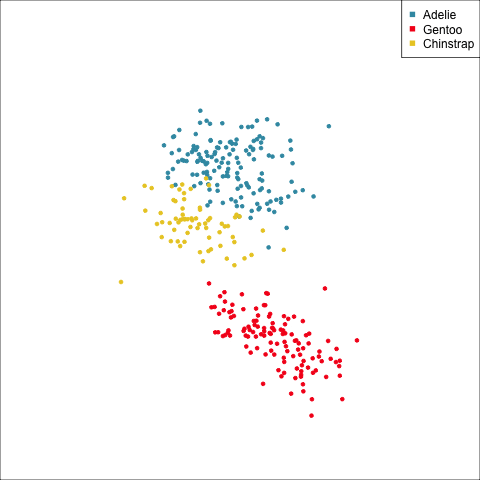
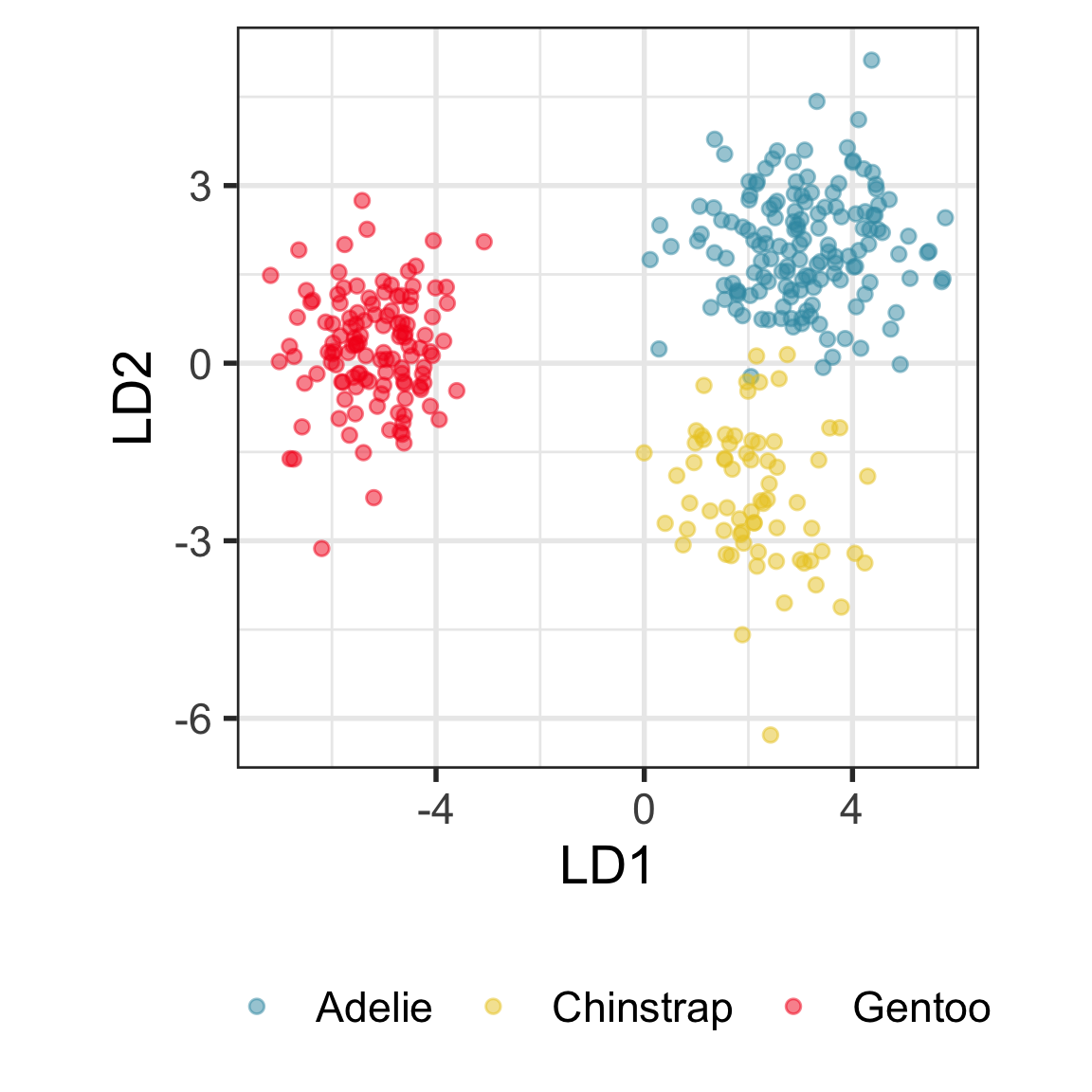
Linear discriminant analysis is the ideal classifier for this data.
Random forests (1/2)
A random forest is the simplest classifier to fit for complicated boundaries. It is built from multiple trees generated by randomly sampling the cases and the variables. The random sampling (with replacement) of cases has the fortunate effect of creating a training (“in-bag”) and a test (“out-of-bag”) sample for each tree computed. The most beautiful results are obtaining diagnostics that help us to assess the model are the votes, the measure of variable importance, and the proximity matrix.
Call:
randomForest(formula = cause ~ ., data = bushfires_sub, importance = TRUE)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 7
OOB estimate of error rate: 11%
Confusion matrix:
accident arson burning_off lightning
accident 73 3 0 62
arson 11 8 1 17
burning_off 3 0 3 3
lightning 14 0 0 823
class.error
accident 0.471
arson 0.784
burning_off 0.667
lightning 0.017Random forests (2/2)
The votes matrix can be considered to be predictive probabilities, where the values for each observation sum to 1. With 3 classes it is a 2D triangle. For 4 or more classes it is a simplex and can be examined in a tour.
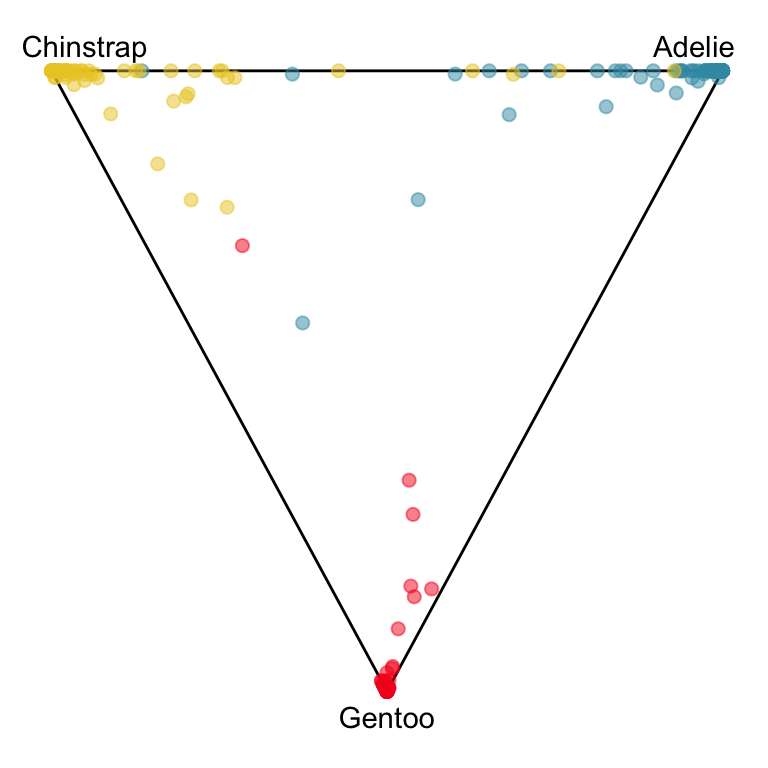
Votes matrix for bushfire model fit
Code
# Create votes matrix data
bushfires_rf_votes <- bushfires_rf$votes %>%
as_tibble() %>%
mutate(cause = bushfires_sub$cause)
# Project 4D into 3D
proj <- t(geozoo::f_helmert(4)[-1,])
b_rf_v_p <- as.matrix(bushfires_rf_votes[,1:4]) %*% proj
colnames(b_rf_v_p) <- c("x1", "x2", "x3")
b_rf_v_p <- b_rf_v_p %>%
as.data.frame() %>%
mutate(cause = bushfires_sub$cause)
# Add simplex
simp <- simplex(p=3)
sp <- data.frame(simp$points)
colnames(sp) <- c("x1", "x2", "x3")
sp$cause = ""
b_rf_v_p_s <- bind_rows(sp, b_rf_v_p) %>%
mutate(cause = factor(cause))
labels <- c("accident" , "arson",
"burning_off", "lightning",
rep("", nrow(b_rf_v_p)))
animate_xy(b_rf_v_p_s[,1:3], col = b_rf_v_p_s$cause,
axes = "off", half_range = 1.3,
edges = as.matrix(simp$edges),
obs_labels = labels)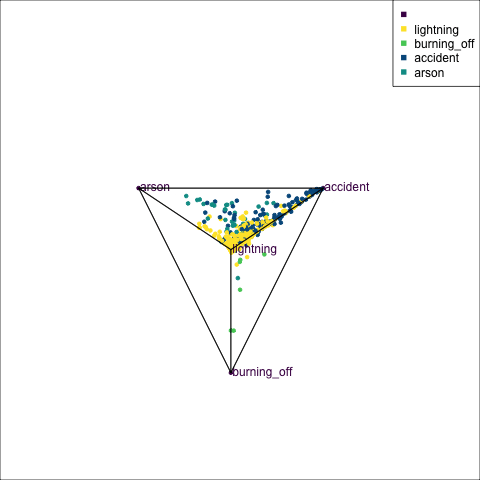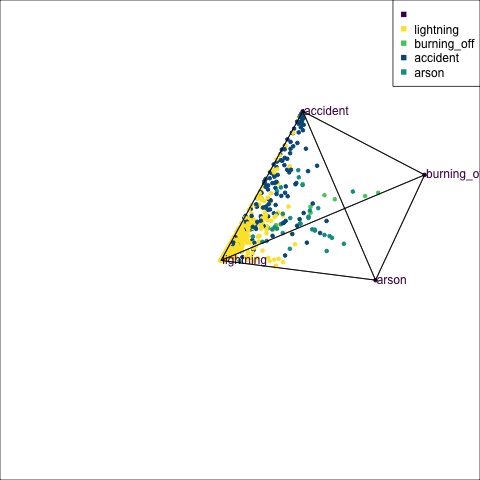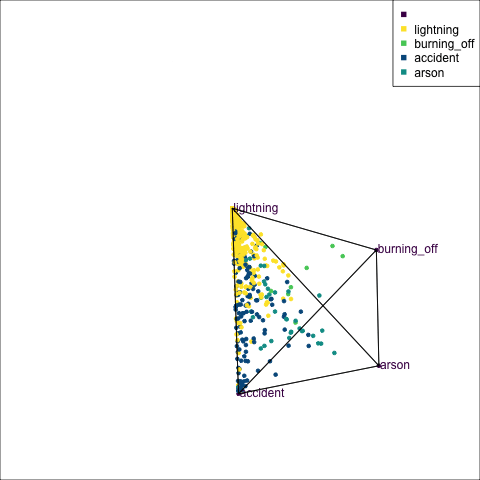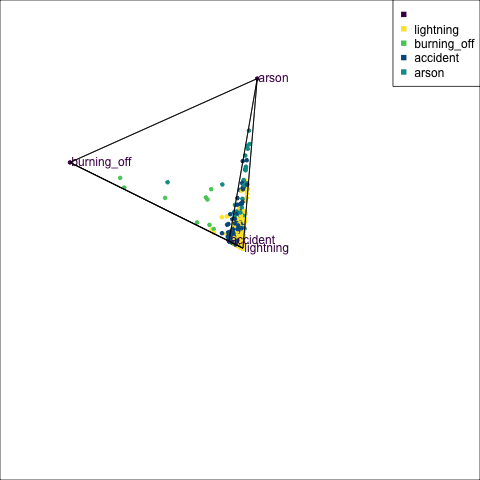
Exploring misclassifications
library(crosstalk)
library(plotly)
library(viridis)
p_cl <- p_tidy_std |>
mutate(pspecies = predict(p_lda, p_tidy_std)$class) |>
dplyr::select(bl:bm, species, pspecies) |>
mutate(sp_jit = jitter(as.numeric(species)),
psp_jit = jitter(as.numeric(pspecies)))
p_cl_shared <- SharedData$new(p_cl)
detour_plot <- detour(p_cl_shared, tour_aes(
projection = bl:bm,
colour = species)) |>
tour_path(grand_tour(2),
max_bases=50, fps = 60) |>
show_scatter(alpha = 0.9, axes = FALSE,
width = "100%", height = "450px")
conf_mat <- plot_ly(p_cl_shared,
x = ~psp_jit,
y = ~sp_jit,
color = ~species,
colors = viridis_pal(option = "D")(3),
height = 450) |>
highlight(on = "plotly_selected",
off = "plotly_doubleclick") %>%
add_trace(type = "scatter",
mode = "markers")
bscols(
detour_plot, conf_mat,
widths = c(5, 6)
) Your turn
Explore the misclassifications in the random forest fit of the penguins data, using the code provided in the slides2.R file.
05:00 Cautions about high-dimensions
Other compelling pursuits
Explore and compare the boundaries of different models using the slice tour.
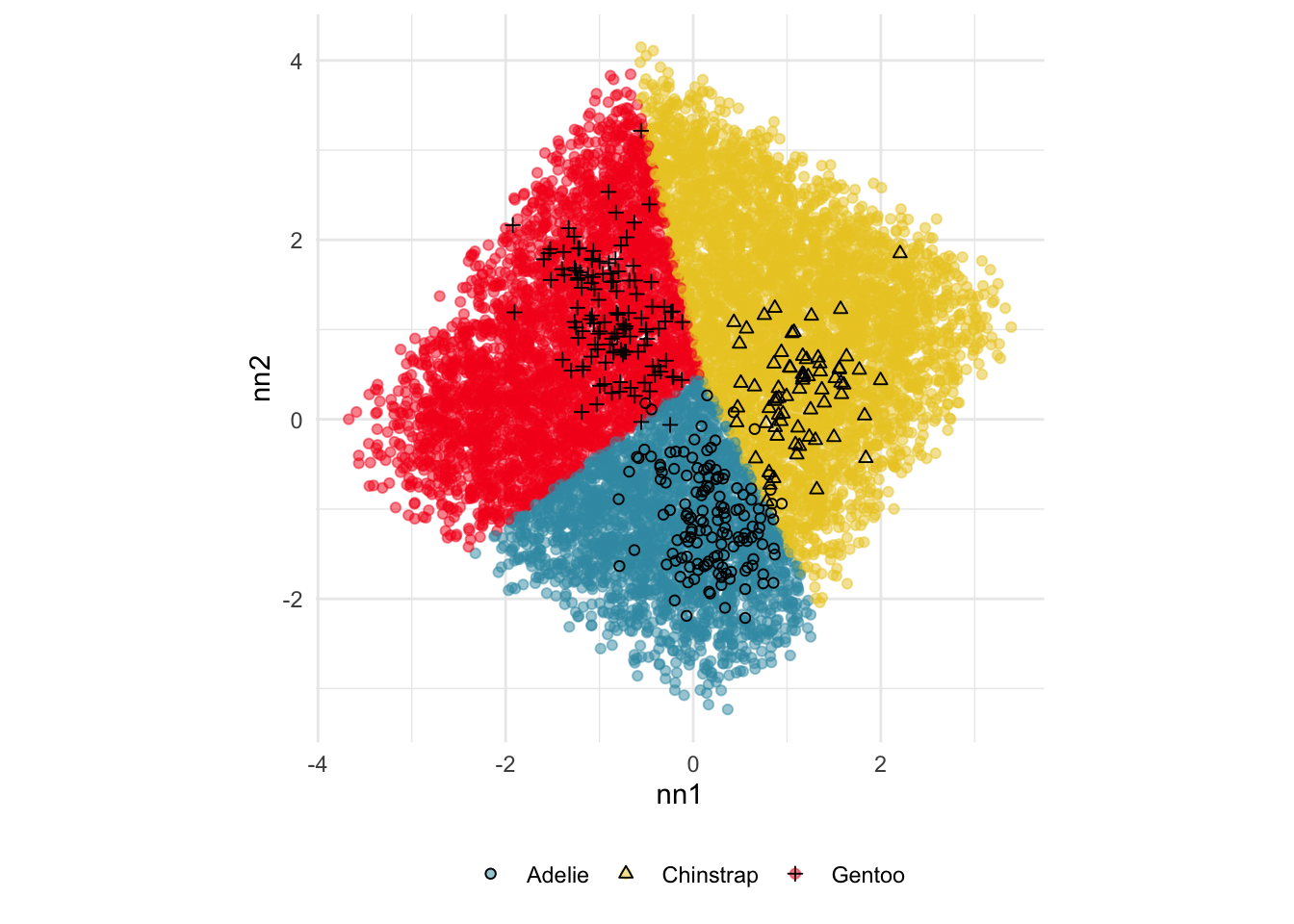
Dissect and explore the operation of a neural network.
Where to learn more
All of the material presented today comes from
Cook and Laa (2024) Interactively exploring high-dimensional data and models in R
Software:
\(~~\) 
\(~~\) 
\(~~\) 
\(~~\) 
End of session 2
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Visualising High-dimensional Data with R Dianne Cook Monash University